How to design ReLu using bitwise operations?

We can simply design ReLu in C as below:

int relu(int x) {
	if (x < 0) 
	   return 0;
	else
	   return x;
}

However, from a hardware perspective, this type of coding can be very inefficient. Imagine that this type of code is compiled and implemented in hardware via an ISA. Each instruction implemented in an assembler has a structure that takes several clocks to complete instead of just one clock. This structure also allows multiple instructions to be executed simultaneously to increase efficiency.

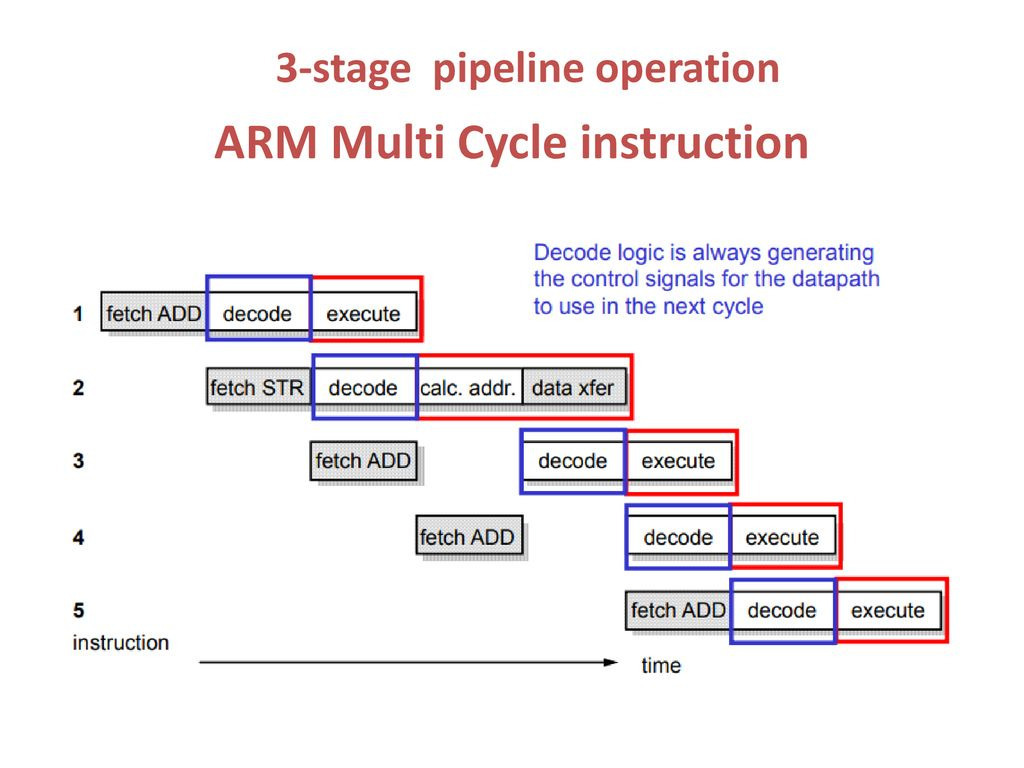
In the pipeline above, we can see that the decode process of the STR instruction and another ADD instruction are performed at the same time that the ADD instruction is entered and the execute process is being performed. With this type of pipeline, we can expect low Clock Cycles per Instruction (CPI).

However, this pipeline is difficult to apply to code that has branches that move memory locations, such as the previous code. Therefore, it is advantageous to write hardware-optimized code that uses as few branching statements as possible. So how do we create ReLu code that is branch-free?

void arm_relu_q7(int8_t *data, uint16_t size)
{
...
    /* Run the following code for M cores with DSP extension */

    uint16_t i = size >> 2;
    int8_t *input = data;
    int8_t *output = data;
    int32_t in;
    int32_t buf;
    int32_t mask;

    while (i)
    {
        in = arm_nn_read_s8x4_ia((const int8_t **)&input);

        /* extract the first bit */
        buf = (int32_t)ROR((uint32_t)in & 0x80808080, 7);

        /* if MSB=1, mask will be 0xFF, 0x0 otherwise */
        mask = QSUB8(0x00000000, buf);

        arm_nn_write_s8x4_ia(&output, in & (~mask));

        i--;
    }

    i = size & 0x3;
    while (i)
    {
        if (*input < 0)
        {
            *input = 0;
        }
        input++;
        i--;
    }
    
 ...

The code above is part of the arm_relu_q7 function in the CMSIS-NN Library provided by ARM. In a nutshell, it takes 8 bits of data, 4 by 4, from the arm_nn_read_s8x4_ia function. Each 32-bit chunk is then ANDed with the constant 0x80808080 and right-shifted by 7 bits to extract the sign bit of each 8-bit value.

Specifically, consider 0x80 in binary: 0b10000000. This represents a negative number in 8-bit signed format. After shifting it 7 bits to the right, it becomes 0b00000001. In other words, the sign bit is effectively moved into the least significant bit position.

Next, we subtract this shifted value from 0x00000000, creating a mask based on the sign:

• For a negative input: 0b00000000 - 0b00000001 = 0b11111111
• For a positive input: 0b00000000 - 0b00000000 = 0b00000000

Finally, applying a bitwise AND between the bitwise NOT of the mask and the original input effectively implements the ReLU function:

• If the input is negative → result becomes 0
• If the input is positive → result remains unchanged

By using bitwise operations in this way, we can implement the ReLU function efficiently without any conditional branching, which is particularly useful for hardware-optimized and low-latency inference.