Harmonic in speech processing

When I started working in the audio group, I often heard people mention the term harmonic in the context of speech processing. Something like the harmonics become stronger when this solution is applied or the lower harmonics are emphasized were. At first, I wasn’t sure what they meant.

According to Wikipedia, a harmonic is defined as “a sinusoidal wave with a frequency that is a positive integer multiple of the fundamental frequency of a periodic signal”. In other words, harmonics are a collection of frequency components that include the fundamental frequency and its integer multiples. The fundamental frequency is the lowest frequency of a periodic waveform, and the human voice is, essentially, a complex periodic waveform.

As we know from the Fourier series, any periodic signal can be decomposed into a sum of sinusoidal signals. The formula is typically written as:
\(\begin{align} x(t) = \sum_{n=-\infty}^{\infty}{c_ne^{j2{\pi}nF_0t}} \end{align}\)

This equation shows that a periodic signal contains only frequencies that are integer multiples of the fundamental frequency $F_0$.

So now we understand why harmonics naturally occur in periodic signals. But this raises another question: Why is the human voice a periodic waveform?

The answer is quite straightforward: the vocal folds (or vocal cords) generate sound by vibrating periodically. This periodic vibration results in a waveform with a clear fundamental frequency and its harmonics. We can actually visualize these harmonics in a spectrogram of human speech, where the horizontal bands represent harmonic components.

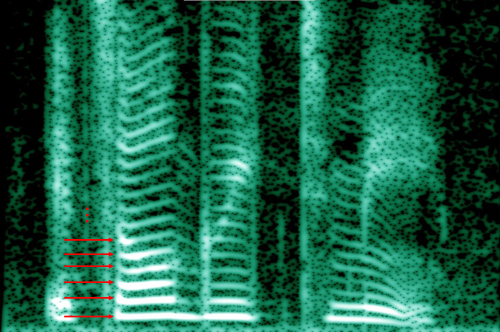
In speech processing tasks such as noise reduction or source separation, recovering or preserving harmonic structures is very important. Harmonics hold essential information about the pitch and tone of the voice, and they can affect perceived quality and intelligibility.